Recursos para calcular las distancias en matemáticas y su aplicación en el aula
Cuando hablamos de “distancia”, rara vez pensamos que estamos usando un concepto profundamente matemático. Desde medir cuán lejos está una ciudad hasta calcular la trayectoria de un dron, la idea de distancia está presente tanto en el mundo físico como en el digital.
© ADOBE STOCK
En geometría, física, informática, navegación o diseño gráfico, la distancia entre dos puntos no es solo una medida: es una herramienta clave para entender relaciones, trayectorias y estructuras.
Existen diversas formas de “medir” la distancia. No siempre se trata de la línea recta más corta. Dependiendo del contexto, existen modelos que pueden ser más útiles o realistas.
La distancia euclidiana es la más común y la que todos conocemos intuitivamente: es la línea recta más corta entre dos puntos. En el plano cartesiano, si tenemos dos puntos la fórmula es:
Esta fórmula es una aplicación directa del Teorema de Pitágoras, que nos recuerda, que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Ejemplo práctico:
¿Cuál es la distancia entre los puntos A(2,3) y B(7,11)?
Aplicando la fórmula:
Este tipo de cálculo es común en física para hallar trayectorias, o en programación para calcular colisiones o cercanía entre objetos.
2. Distancia de Manhattan
También llamada “distancia L1” o “distancia de taxi”, se usa en contextos urbanos (como recorrer calles).
Ejemplo: Entre los puntos A(2,3) y B(7,11)
d=|7-2|+|11-3|=5+8=13
3. Distancia de Chebyshev
Usada en ajedrez (el movimiento de la reina) o en algoritmos que permiten movimiento diagonal.
Ejemplo:
d=max(5,8)=8
4. Distancia tridimensional
Para puntos en el espacio A(x1, y1, z1) y B(x2, y2, z2)
Ejemplo: Entre A(1,2,3) y B(4,6,8)
Tabla comparativa de fórmulas
| Tipo de distancia | Fórmula | Uso común |
|---|---|---|
| Euclidiana | 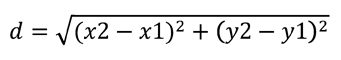 | Geometría, física, gráficos |
| Manhattan | 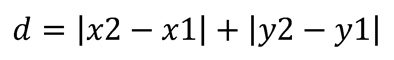 | Planificación urbana, robótica |
| Chebyshev | 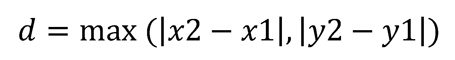 | Ajedrez, estadística |
| Tridimensional | 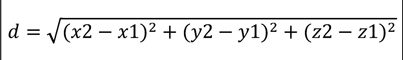 | Física, ingeniería, realidad 3D |
| Tipo de distancia | Fórmula | Uso común |
| Euclidiana | —————– | Geometría, física, gráficos |
| Manhattan | ——————- | Planificación urbana, robótica |
| Chebyshev | ——————- | Ajedrez, estadística |
| Tridimensional | —————— | Física, ingeniería, realidad 3D |
4. Ejercicios y problemas para el aula
Proponemos estos ejercicios para trabajar en clase o como práctica:
- Calcula la distancia euclidiana entre los puntos A(3,5) y B(−2,9).
- ¿Cuál sería la distancia de Manhattan entre esos mismos puntos?
- Compara las tres distancias (euclidiana, Manhattan y Chebyshev) entre A(4,4) y B(9,8).
- Encuentra la distancia entre A(1,2,1) y B(4,6,2).
Explorar diferentes formas de medir distancia ayuda al alumnado a comprender que las matemáticas no son un conjunto de reglas fijas, sino una herramienta adaptable según el problema y el entorno.
¿Cuál de estas distancias has enseñado en clase?, ¿Has usado software como Excel o GeoGebra para representarlas? ¡Esperamos tus ideas y comentarios para seguir construyendo juntos una didáctica más conectada, visual y motivadora!
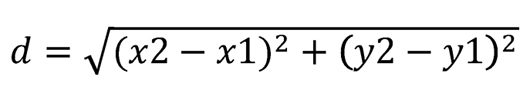
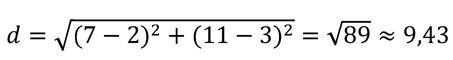
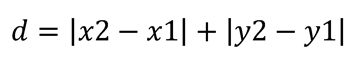
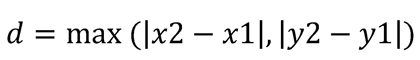
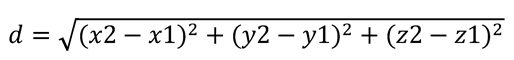
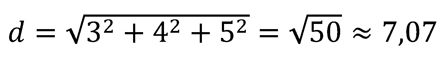
Gracias, por lo que he aprendido sobre la uti.lidad y fór,ulas, para el cáculo de otras distancias. distinta de la euclidiana, tal y como demuestran las interesantes variaciones sobre un mismo problema de las diferentes medidas. MI agradecimiento a la autora.
En ajedrez se usa mucho el método de la distancia de Chebyshev porque modela perfectamente el movimiento del rey.
Muchas gracias, Seve. Con lo que he jugado al ajedrez, e incluso e participado en un campeonato entre profesores y alumnos y nunca había oído esa medida,
Muy buena la tabla comparativa de fórmulas que has propuesto.