Enseñar el Teorema de Pitágoras con Bhaskara

Bhaskara II fue uno de los matemáticos más influyentes de la India antigua. Vivió en el siglo XII y dejó importantes aportes en aritmética, álgebra, geometría, astronomía e incluso cálculo. En su trabajo, destinado a la enseñanza de las matemáticas, incluye una elegante demostración del Teorema de Pitágoras que sigue fascinando a docentes y estudiantes hasta el día de hoy.

Esta prueba se basa en una construcción geométrica muy sencilla, presentando un diagrama, que se basa en el poder visual del razonamiento.

La idea es la siguiente:

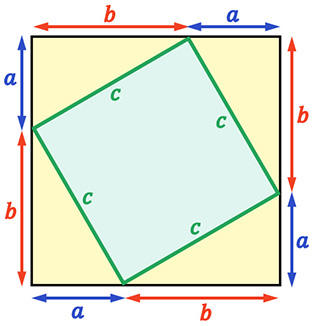
1. Se construye un cuadrado grande de lado (a+b), donde a y b son los catetos de un triángulo rectángulo.
2. Dentro de este cuadrado, se colocan cuatro triángulos rectángulos congruentes, dejando en el centro un cuadrado más pequeño.
3. Este cuadrado central tiene por lado la hipotenusa c del triángulo.

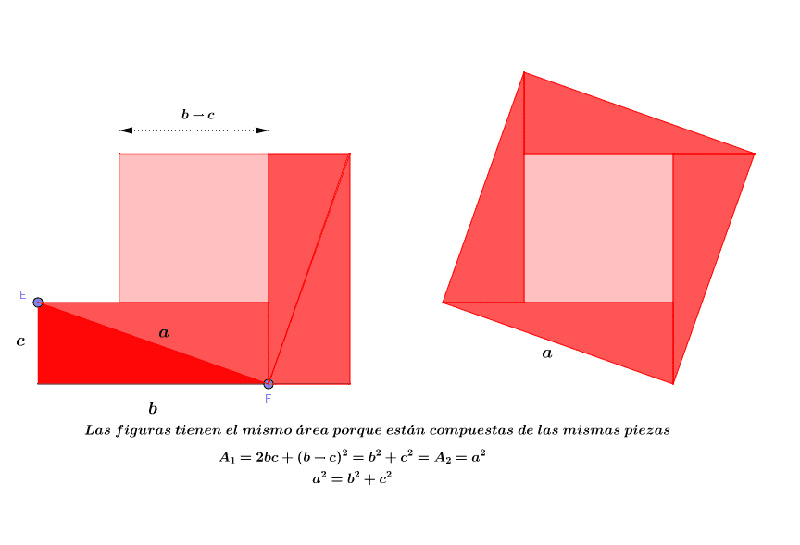
La clave está en observar que el área total del cuadrado grande se puede expresar de dos formas:

• Como un solo cuadrado: (a+b)²
• Como la suma del área de los cuatro triángulos y el cuadrado interior: 4 (½ ab) + c²

Igualando ambas expresiones se obtiene:

(a + b)² = 2ab + c²

Desarrollando el cuadrado del lado izquierdo:

a² + 2ab + b² = 2ab + c²

Restando “2ab” a ambos lados:

a² + b² = c²

Y así, de manera simple y visual, se demuestra el Teorema de Pitágoras.

Lo maravilloso de esta demostración es que no depende del lenguaje algebraico complejo. Puede utilizarse con estudiantes que aún no manejan el álgebra de forma avanzada, ya que pueden observar el razonamiento geométrico directamente.

Algunas ideas para llevarla al aula:

Material manipulativo

Puedes pedir a tus estudiantes que construyan el cuadrado grande con papel de colores, recortando los triángulos y armando el rompecabezas. Ver cómo encajan las piezas refuerza la comprensión de la igualdad de áreas.

Aprendizaje visual y colaborativo

Invita a tus alumnos a describir en sus propias palabras lo que observan en el diagrama. ¿Cómo explicarían que los triángulos dejan un cuadrado perfecto en el centro? ¿Qué relación descubren?

Desafío creativo

Propón a los estudiantes que inventen su propia forma de demostrar el teorema usando recortes, figuras o tecnología (como GeoGebra). Esto estimula el pensamiento crítico y la creatividad.

Contextualización histórica

Aprovecha la historia de Bhaskara para destacar cómo distintas culturas han contribuido a las matemáticas. Este enfoque humaniza la disciplina y abre la puerta a la reflexión intercultural.

Demostrar el Teorema de Pitágoras no debería ser un ejercicio reservado a niveles avanzados. Con recursos visuales como el de Bhaskara, es posible llevar la comprensión conceptual a todos los niveles, mostrando que las matemáticas no son solo fórmulas, sino también razonamientos, belleza y conexiones.

Esta demostración ofrece a los estudiantes algo más que una técnica: les brinda una idea poderosa que pueden visualizar, explicar y recordar.

¿Conocías la prueba de Bhaskara?, ¿La has utilizado en el aula?, ¿Cómo reaccionaron tus estudiantes? Te invitamos a compartir tu experiencia en los comentarios. ¡Tu práctica puede enriquecer la de otros docentes!