Cómo representar una función: siete pasos para garantizar el éxito en Bachillerato

Paso 1: Estudio del Dominio

El primer paso consiste en definir el dominio de la función. Esto implica identificar los valores de la variable independiente “x” para los cuales la función está definida. Con esta información, se delimitan las regiones del plano donde la función existe.

Paso 2: Puntos de Corte con los Ejes

Determinar los puntos de intersección de la función con los ejes de abscisas y ordenadas es crucial para su representación. Se trata de obtener los valores para los cuales la función se anula (corte con el eje X) y los valores de “y” cuando “x” es cero (corte con el eje Y). Dichos puntos son esenciales para esbozar la gráfica de la función.

Paso 3: Simetrías

Las funciones pueden presentar simetrías que son clave para su representación gráfica. Una función es par si muestra simetría respecto al eje Y (f(-x) = f(x)), e impar si su centro de simetría es el origen (f(-x) = -f(x)). Identificar la presencia o ausencia de simetrías ayuda a simplificar el proceso de representación.

Paso 4: Asíntotas

Las asíntotas pueden ser de tres tipos, y su identificación es crucial para entender el comportamiento límite de la función:

Asíntotas horizontales: La recta y=k es una asíntota horizontal de la función si se cumple: 

Asíntotas verticales: La recta x=k es una asíntota vertical de la función si se cumple:

Asíntotas oblicuas: Cabe destacar que, si existen asíntotas horizontales, no habrá asíntotas oblicuas. Se trata de una recta representada como y=mx+n, siendo:

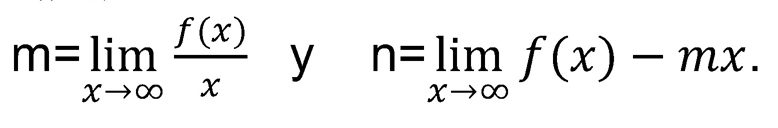
La existencia de asíntotas aporta información muy valiosa sobre el comportamiento de la función en los extremos del dominio.

Paso 5: Monotonía

La monotonía de una función describe su tendencia al crecimiento o decrecimiento. Este comportamiento se determina calculando la primera derivada (f´(x)) y evaluando el signo que presenta:

• Si f´(x)>0, la función es creciente.
• Si f´(x)<0, la función es decreciente.

Además de analizar los intervalos de crecimiento y decrecimiento, se puede identificar la presencia de posibles máximos y mínimos, anulando esta primera derivada (f´(x)=0). Para saber si los puntos obtenidos son máximos o mínimos, se realiza una segunda derivada de la función, f´´(x):

• Si f´´(x)<0, se trata de un máximo.
• Si f´´(x)>0, se trata de un mínimo.

Paso 6: Curvatura

El estudio de la curvatura aborda la concavidad y convexidad de la función, además de los puntos de inflexión que pueda presentar. Se trata de calcular la segunda derivada de la función, y observar:

• Si f´´(x)>0, es convexa.
• Si f´´(x)<0, es cóncava.
• Para calcular los puntos de inflexión, bastaría con obtener los valores de “x” que anulen la segunda derivada: f´´(x)=0.

Esta información añade detalle y precisión al esbozo de la gráfica.

Paso 7: Representar un Cuadro de Valores

Finalmente, se recomienda organizar todos los datos recopilados en un cuadro de valores. Este resumen sirve como una herramienta de verificación y asegura que todos los aspectos relevantes de la función han sido considerados antes de proceder a su representación gráfica.

La representación de funciones es más que un ejercicio matemático; es una ventana hacia el entendimiento de las relaciones cuantitativas y su impacto en el mundo real. Esperamos que esta guía facilite el proceso de enseñanza y haga de la representación de funciones una tarea más accesible y menos intimidante para los estudiantes. ¿Te ha resultado interesante? ¡Comparte tus propios pasos para representar funciones en los comentarios! ¡Juntos, podemos enriquecer nuestro enfoque didáctico y motivar a los estudiantes en su aprendizaje!